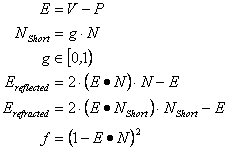Soft objects

Using the marching cubes algorithm allows us to generate the polygonal contour (called iso-surface) of a 3D density field for a given density threshold. Refer to [1] for an algorithm description which also includes an implementation in C/C++. The density data can either come from 3D volumetric data sets (e.g. taken from MRI scans) or it can be expressed implicitly by a mathematical function. In our case we use a simple function to describe a single blob in the scene. Other functions for modeling soft objects can be found in [2].

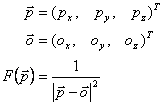
Density function

F returns the density value at p for a blob with origin o which is simply the inverse of the squared Euclidian distance between p and o. The advantage of having a formula is the ease at which surface normals can be calculated. There is no need to approximate surface normals as described in [1]. By calculating the partial derivative of F we can express the normal N for a given point p in space directly. Having correct normals is crucial for shading the surface.

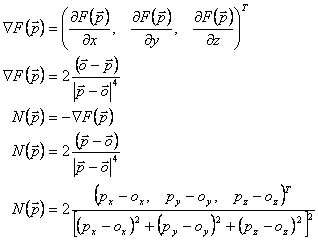
Normal of density function

For more complicated density functions N can be approximated in the following way.

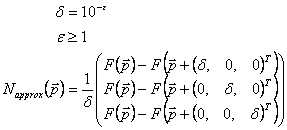
Approximated normal of density function

By taking several individual blobs and adding up their density functions it is possible to build complex soft objects. The normal at a given point p in space is also just the sum of N for each blob.

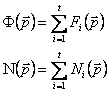
Density function and its normal of a blobby object

We tessellate our soft objects using a special version of the marching cubes algorithm. Instead of performing the algorithm for each and every voxel of a 3D volume we trace a line from the center of each blob out until it intersects the surface. If the voxel belonging to the intersection point hasn't been tessellated yet we compute the polygonal surface for it and then progress to its neighbors until all interlinked voxels have been visited. Otherwise the blob penetrates another one which has already been processed. An algorithm outline can be found in [3].

After tessellation the polygonal contour is rendered using a shader taking reflected and refracted light into account to visualize translucent matter. It's the vertex shaders responsibility to calculate the reflected view vector and an approximation of the refracted view vector for each vertex. Also, a coarsely approximated fresnel term is computed to allow the pixel shader to blend between the corresponding color values for both the reflected and refracted view vector taken from an environment map.

for a given point P on a surface
V	viewer position
E	vector to viewer for P
N	surface normal for P
f	fresnel term for P

References

	[1] Paul Bourke. "Polygonising a scalar field"
	[2] Paul Bourke. "Implicit Surfaces"
	[3] Andreas Jönsson. "Fast metaballs"

Last update on 2002-03-17
Meshuggah Demo and Effect browser.