Ocean scene

The Ocean scene is the most complex effect in Meshuggah both visually/computationally and in terms of using shaders. It's based on the papers [1] and [2] I came across lately. The provided sample shots there looked promising enough to give it a shot. The implementation given here also utilizes simplified equations from [4] to determine the view dependent color of water (pre-calculated and stored in a texture) and a contrast-enhancement approach based on [3] to further improve the visual results when rendering ocean water.

First and foremost a realistic model for simulating and animating ocean water is necessary to generate an appropriate mesh used for rendering. [1] and [2] - in greater detail - describe a statistical model based on observations of the real sea. It has been successfully used commercially in feature movies such as Titanic and Waterworld. In this model a wave height field is decomposed into a set of sinus waves with different amplitudes and phases. While the model itself provides formulas to generate these amplitudes and phases an inverse Fast Fourier Transformation (FFT) converts them back into the spatial domain, thus creating a wave height field required for building the ocean mesh. It also allows calculating proper normals and displacement vectors for the height field. These are used to shade the ocean mesh and to form choppy waves.

A big advantage of this particular model is that it produces an ocean height field which tiles perfectly. In Meshuggah a 64 x 64 ocean height field is repeated four times both horizontally and vertically to form a 256 x 256 ocean mesh.

What contributes to the look of the ocean surface? At first we need to determine the color of water. As mentioned above we can take the equations provided in [4] and simplify them by treating the water surface as a flat plane. The result is an equation only depending on the angle between the viewer and a point p and its normal n on the ocean surface. It can be pre-calculated as a 1D lookup texture containing greenish colors for angles of about 90 degrees (viewer looks over wave) and dark blue colors for angles near or equal to zero degree (viewer look straight on wave). In Meshuggah a simple linear interpolation between the two colors using the angle between view vector and wave normal as a blend factor has to be calculated instead since all available texture address operations are already reserved for other purposes and an extra render pass was avoided for performance reasons. Another factor which should be taken into account is reflected skylight. To further enhance the detail of the water surface the reflections will be per-pixel based meaning that the viewer will be able to see little ripples on the water surface coming from a dynamically updated bump map. In order not to overemphasize the reflections we also need to calculate the fresnel term for the air to water case, multiply it to the reflected color and add the result to the color of water. Otherwise reflections would make the water look more like liquid metal instead. [1] proposed the following approximation:

The fresnel term is a good candidate for performing contrast enhancement. In [3] an exposure factor is multiplied to a high dynamic range texture map (16bit information per color channel). In our case the fresnel term influences how much reflected light should be added to the color of water for a given pixel. By multiplying an exposure factor to the fresnel term we can increase the intensity in areas of the ocean surface where sunlight is reflected while leaving other areas relatively dark. Register combiners and final multipliers are used in [3] to overcome the limited range of [0..1] for input colors and color math. We use pixel shader instruction and their modifiers which are basically just an abstraction of both. In the vertex shader we calculate the fresnel term and multiply it by a constant exposure factor. In Meshuggah it is limited [0..4] to save pixel shader instructions as we will see later. Since output color registers oD0 and oD1 will clamp any value passed to them to [0..1] before they are interpolated during rasterization and sent to the pixel shader we need to split up our exposure times fresnel term. The fractional portion of it will be extracted and copied to oD1. The integer portion is divided by the maximum exposure value - 4 in our case- and copied to oD0. This way we avoid any clamping of color values. In the pixel shader we combine the exposure times fresnel term with the color from the environment map representing reflected skylight. At first we multiply the color from the environment map by v0 (corresponds to oD0) and use _x4 instruction modifier to even out the division which was performed when splitting up the exposure times fresnel term in the vertex shader. Then we multiply the color from the environment map by v1 (corresponds to oD1) and add it to the previous result. This yields in the desired reflected skylight times fresnel term times exposure factor color which is added to the color of water.

Doing per pixel reflections using a bump map requires to setup a transformation matrix in the vertex shader which is used to transform normals fetched from the bump map into world space so that  the view vector is reflected correctly. Normals in the bump map are stored in a way that no transformation would be necessary if the ocean surface would be a flat (x/z) plane. That is, they correspond with our (left-handed) world coordinate system. Since our ocean mesh is based on a height field which in turn is based on a rectangular grid generating the transformation matrix is easy. It's formed by three normalized (!) vectors x, y and z which are copied into three consecutive output texture registers (namely oT1 - oT3 as oT0 is reserved for bump map texture coordinates).

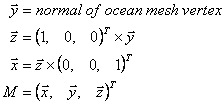
During rasterization the pixel shader receives an interpolated version of these three vectors representing a per pixel transformation matrix to transform the bump map normal from texture into world space. To create and update the bump map every frame normals from our current ocean height field can be used. Since these normals already represent an ocean surface they can be used to model surface detail at a lower scale as well. Therefore the bump map is tiled multiple times over the ocean mesh.

As a last note a curvature is applied to the ocean mesh in the vertex shader. It's based on the x/z distance of each ocean mesh vertex to the viewer's current position.

References

Last update on 2002-03-17

 

Meshuggah Demo and Effect browser.

Copyright © 2001, 2002 Carsten Wenzel.

All rights reserved.